The Calendar gadget in the Windows Sidebar may display blank content, showing only the plain orange background. Also, the Stocks Gadget may not show up when you add it to the Sidebar. This problem is usually caused by a missing scripting run-time registration.
Registering VBScript.DLL
Registering the vbscript.dll file from an admin Command Prompt fixes the problem. Follow these steps:
1. Open an Admin Command Prompt window. To do so, click Start, click All Programs, click Accessories, right-click Command Prompt, and then click Run as Administrator.
2. Type the following command and press ENTER:
You should see the following message after running the command:
DllRegisterServer in vbscript.dll succeeded.
3. Restart Windows and see if the Calendar and Stocks Gadgets render correctly.
That doesn’t help? Fix the Zones Registry Key
Of late, we’ve seen several cases where an additional IE Security Zone registry key causing this problem. The additional security zone may have been added by a Malware, could appear as a pseudo-graphic number listed before zone number 0. The fix listed below is the same as the one documented in post Gadgets are Not Displayed Correctly in Windows 7 and Windows Vista.
Run the Fix-It Solution from Microsoft
[Windows 7 Users] Download the Fix it solution by clicking the image above, and run the executable. The problem should be taken care of, automatically.
To Fix the Problem Manually
1. Click Start, type Regedit.exe and press {ENTER}
2. Navigate to the following branch:
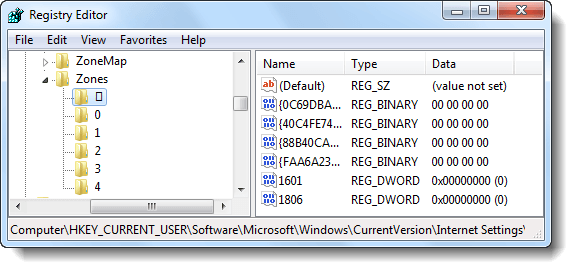
3. Under the Zones key, delete the subkey shown with an ASCII character, as in the above graphic.
4. Exit the Registry Editor.
5. Logoff and login back to your account.
Still doesn’t work after trying the above steps? Drop your comment below, and let’s see if we can work on this issue further.
Related Posts
- How to Fix Sidebar Crash “Windows Desktop Gadgets Has Stopped Working”
- How to Use Sidebar 32-Bit Mode in Windows 7 and Windows Vista 64-Bit Editions to Run Silverlight Gadgets
- Fix Currency, Stock or Weather Gadgets Not Updating in Windows 7 and Windows Vista
- Why There Are Two Instances of Sidebar.exe Running
- Installation of Windows Sidebar Gadgets Is Managed by Your System Administrator
If you enjoyed this post, make sure you subscribe to our RSS feed! We feature Tips, Troubleshooting information, Scripts and Utilities for Microsoft Windows Operating Systems!
Prefer an E-mail subscription?
Thanks, Paul – good catch! Copy&Paste from my reg key export did me in.
My post should read:
[HKEY_CLASSES_ROOT\CLSID\{B54F3741-5B07-11cf-A4B0-00AA004A55E8}\InprocServer32]
@=”C:\Windows\system32\vbscript.dll”
“ThreadingModel”=”Both”
Make sure that the default value is –> ”C:\Windows\system32\vbscript.dll”
— Larry, below, had issues with Avast as well. I’d not be surprised if the vast majority of people here had a similar problem with a script-blocking component of an AV app.
FYI – Avast AV does the same thing.
Also, make sure it’s “C:\Windows\system32\vbscript.dll” not “C:\\Windows\\system32\\vbscript.dll”
Those who are still having problems should doublecheck to be sure that they are not having the issues that Larry and I had with the uninstall of an anti-virus program.
When I uninstalled the trial Mcafee AV on my computer, it left this registry key with the wrong default value:
[HKEY_CLASSES_ROOT\CLSID\{B54F3741-5B07-11cf-A4B0-00AA004A55E8}\InprocServer32]
@=”C:\\Program Files\\Common Files\\McAfee\\SystemCore\\ScriptSn.20110222204811.dll”
“ThreadingModel”=”Both”
The default value needed to be changed back to the value below:
[HKEY_CLASSES_ROOT\CLSID\{B54F3741-5B07-11cf-A4B0-00AA004A55E8}\InprocServer32]
@=”C:\\Windows\\system32\\vbscript.dll”
“ThreadingModel”=”Both”
Make sure that the default value is –> ”C:\\Windows\\system32\\vbscript.dll”
Best of luck to all :)
No subkey shown with an ASCII characte rthe regedit and that ascii “numbered” zone wasn’t there.
Still Calendar Gadget in Windows Sidebar Is Blank With Orange Background..
System unable to install fix it??
Please help
Kt
said this on Wednesday, March 7th 2012 7:31 am
Drats! I did the first fix, regsvr32.exe vbscript.dll, and got the proper response that the dll reg server succeeded, but saw no change after restarting the computer. So did the regedit and that ascii “numbered” zone wasn’t there. Help! :)
me 2 … :[[ HELP US :[[
Did both steps – but the Regedit.exe where Zone is does not have ASCII character. The dll didnt work either. What’s next please?
Drats! I did the first fix, regsvr32.exe vbscript.dll, and got the proper response that the dll reg server succeeded, but saw no change after restarting the computer. So did the regedit and that ascii “numbered” zone wasn’t there. Help! :)
Thank you, PhilliePhan, that somebody is me! Same issue. My nemesis, however, was Avast. To others who try this solution, you may have to modify the permissions before regedit will let you modify the key. (:)